| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 도쿄스카이트리
- 랄프커피
- 스카이트리
- 생성형ai
- 정처기실기후기
- 마츠리
- adsp시험후기
- 야키토리
- ADsP시험방법
- 정처기실기준비
- 캐릭터스트리트
- 도쿄디즈니랜드
- ~8월까지
- ADsP
- 아자뵤
- 일본편의점
- 오모테산도힐즈
- 오모테산도
- 가라오케
- 목록
- ChatGPT
- 다이마루백화점
- 시부야스크램블교차로
- 일본녹차
- 정처기실기
- 대4인생
- 가보자고
- 키디랜드
- 도쿄여행
- 도쿄아사히
- Today
- Total
+ Repository +
[RL] Ch.4 : Model-free prediction 본문
[RL] Ch.4 : Model-free prediction
jaeti 2021. 5. 11. 15:28* David Silver _ Reinforcement Learning 강의자료를 토대로 공부하여 정리한 내용입니다.
Model-Free : 주어진 environment를 모르는 상황.
MDP : Markov Decision Process

Model-Based인 MDP문제를 푸는 방법에는 (Planning) 이와같이 Prediction과 Control이 있다.
- Prediction : 주어진 policy를 평가하는 것. (value function을 찾는 것)
- Control : Optimal한 policy를 찾아내는 것.
이와같이 Model-Free한 상황에서도 value function을 추정하는 Prediction과, 최적화하는 Control로 나눌 수 있다.
이번장에서 다룰 내용은 MDP를 모르는 상황에서 value function을 추정하는 Model-Free Prediction이다.
여전히 작은 MDP를 다루므로, table look-up 방식을 활용한다.
1. Monte-Carlo Learning
- MC는 각 에피소드를 실행함으로써 경험하여 직접 배운다.
- 한 에피소드를 완전히 끝 냈을 때 학습된다.
- 매우 간단한 아이디어를 사용한다. value = mean return (평균)
- 단, 모든 에피소드가 끝나야 적용 가능하다.
MC Policy Evaluation (Prediction)
- 목적 : policy π에 따른 각 에피소드의 경험치로 Vπ를 학습하는 것.


return값은 매 에피소드마다 다르므로 확률변수이다. (랜덤하게 선택)
∴ 리턴의 기댓값
MC의 종류는 두가지로 나눌 수 있다.
1. First-Visit MC : 한 episode에서 한 state가 여러번 방문됐을 때 첫 한 번만 방문으로 치는 것.

처음 방문했을 때만 counter 올려주고, return값에 더한다.
2. Every-Visit MC : 한 episode에서 한 state가 여러번 방문됐을 때 여러번 다 방문으로 치는 것. 알고리즘 자체는 F.V MC와 동일하다.
둘 다 무한번의 에피소드를 실행하였을 때(누적되는 N(s)), V(s)는 vπ(s)로 수렴하게 된다.
* 이 때, 랜덤한 policy가 골고루 움직여 모든 state를 다 방문한다고 가정한다. N(s) → ∞ 이 되어야하므로.
Incremental Mean
단, 현재의 방법으로는 s라는 변수가 필요하므로 변수없이 바로 value function 계산하는 방법이다.

시간에 따라 확률이 바뀌는 상황에서 (non-stationary problem 등에서) 좋을 수 있다. 최근값에는 a, 그 전 값에는 a^2 등 -.
즉, 이전의 값에 가중치를 더 낮게 책정한다는 의미이다. 최근 값에 가중치 ↑
MC 한줄정리 : 여러번 해보고 평균내기
2. Temporal-Difference Learning
TD는 MC와 다르게 불완전한 에피소드를 통해서 배운다. (Bootstrapping)
즉, 추측치를 통해 추측치를 update하는 학습 방법이다.

여기서

이는 한 스텝 가서 예측한다는 의미로, TD target 이라고 한다.
TD target과 V(St)와의 차는 TD error이다.
TD의 예시 [ Driving Home Example ]

이와 같이 실제로 상태에 이르기까지 총 걸린시간, 내가 예측한 시간, 그 두값의 합을 나타낸 표가 있다.
여기서 'leaving office', 'reach car, raining' 등은 각각의 state가 된다.

이와같이 MC의 경우에는 43분에 한 episode가 종료되었으므로 (끝났으므로), 모든 state가 43분으로 update된다.
하지만, TD의 경우에는 위의 표에서 실제 걸린 시간과 예측시간을 합한 값으로 (즉, 다음의 예측값으로) state들이 update된다.
따라서, TD는 MC와는 다르게 최종적인 결과값이 (끝값에 도달 x) 나오기 전에 학습이 가능하다.
→ MC는 한 에피소드가 완전히 끝날 때 까지 기다렸다가, 끝나면 return값을 가지고 업데이트 함.
∴ TD는 확실하게 끝나는 state가 없는 환경에서도 학습이 가능하다. (non-terminating)
→ MC는 끝이 있는 환경에서만 학습 가능. (terminating)
Bias/Variance Trade-Off
< Bias 관점 >
- MC는 Gt를 무한하게 sampling하여 평균하면 기댓값이 틀림없는(unbiased) Vπ로 수렴한다.
- TD는 만약 확실한 Vπ(St)를 안다면 *TD target으로 업데이트시 틀림없는추정치를 얻어낼 수 있다. (Bellman eq.에 의해 보장)
그러나, 현실적으로 우리는 확실한 Vπ(St)값을 모르니 아무리 학습해도 완벽한 Vπ에 수렴할 수 없다. → Biased하다.
▶ Bias 관점 TD가 MC보다 안좋다.
< Variance 관점 >
variance = 분산, 즉 확률변수에서 얼마나 분포가 퍼져있느냐. (평균이 0일 때, sample1 = -1000, sample2= 1000)
- MC의 return값은 에피소드가 끝날 때 까지 진행하므로 많은 랜덤 변수들에 영향을 받는다.
- TD는 한 번만 랜덤하게 진행하므로, 한 번만 의존함.
▶ Variance 관점 TD가 MC보다 좋다.
| MC (zero bias, high variance) |
TD (some bias, low variance) |
| - 수렴성질 좋다. - 값들을 Q-table에 다 못 넣을만큼 사이즈가 커지면 Neural net 을 이용하는데 (=deep learning), 그 때도 수렴성질 좋다. - initial value 그닥 중요 x |
- 대체로 MC보다 더 효과적이다. - 또, TD(0)는 Vπ(S)에 수렴한다. (함수근사화로) - initial value에 민감하다. (처음에 좋은 추측치 설정되어있으면 그만큼 잘 수렴하므로.) |
* bias 있어도 틀린값으로 인식 안 하고 동작 한다.
유한한 에피소드
무한한 에피소드에서는 MC와 TD 결국 둘 다 V(s) → vπ(s) 로 잘 수렴한다. (같은 값)
하지만, 제한된 에피소드에서는 두 값이 달라진다.
유한한 에피소드 예시 [ batch MC & TD ]

왼쪽에 주어진 action들과 reward들로 오른쪽 그림이 도출된다고 할 때,
- MC로 학습 : V(A) = 0
- TD로 학습 : V(A) = 0.75
이 될 것이다. TD는 현재 액션 스테이트의 reward 받고, 다음 γV(s+1) 을 더해 V(A)를 업데이트 하므로. (0+V(B))
* γ는 1로 가정한다.
따라서, 제한된 episode를 가지는 환경에서는 MC와 TD 두 학습에 대한 v(s)의 수렴값이 달라지게 된다.
| MC | Markov property 관계없이 MSE만을 최소화 |
| TD | Markov environment 사용하여 likelihood를 최대화해 v(s) 추측 |
지금까지의 MC와 TD 총 정리
| Monte-Carlo Backup | Temporal-Difference Backup | Dynamic Programming Backup |
 |
 |
 |
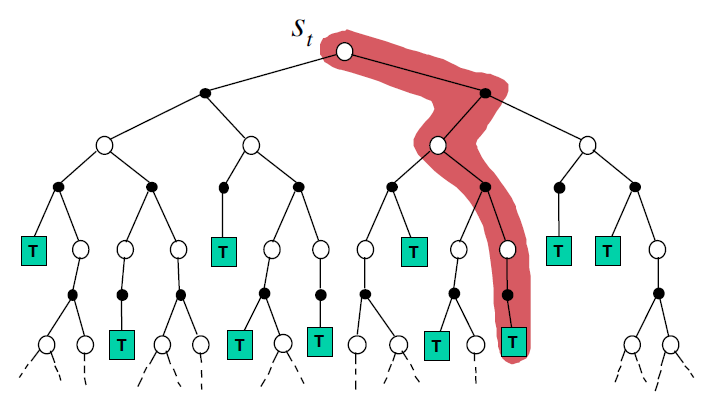 |
 |
 |
- MC : 한 에피소드 끝까지 해보고, 그 때 얻어진 reward값으로 value update 하는 애.
- TD : 한 에피소드 끝까지 안 가고, 한 스텝만 가보고 추측해서 대체. (Bootstrapping)
- DP : sampling 안 하고 (전부 다 해봄), 한 스텝만 가서 value update.
| MC | TD | DP | |
| Bootstrapping | X | O | O |
| Sampling | O | O | X |
* Boothstrapping = depth 관점
* Sampling = width 관점

'강화학습 (Reinforcement Learning) > 이론 (David Silver)' 카테고리의 다른 글
| [RL] Ch.5 : Model-Free Control (0) | 2022.01.07 |
|---|---|
| [RL] Ch.6 : Value Function Approximation (0) | 2021.07.20 |


